정의
트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다.
트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다.
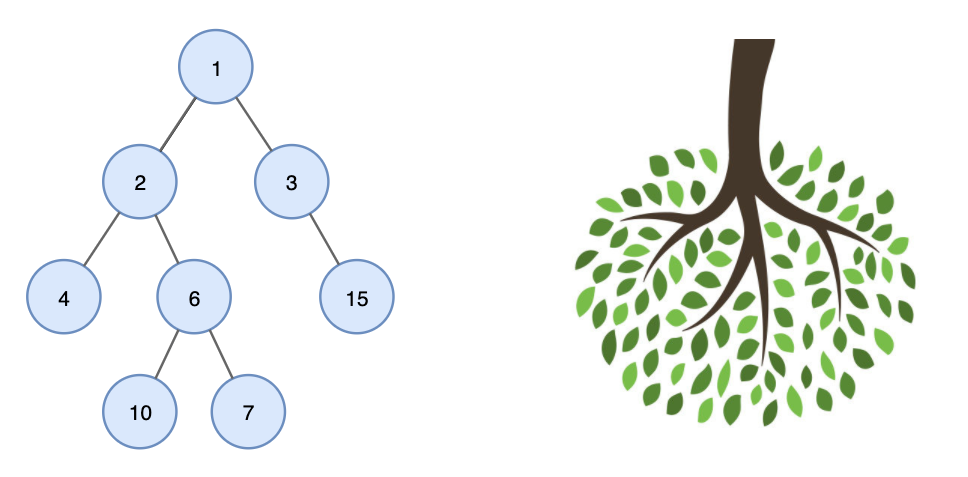
트리는 또한 트리 내에 다른 하위 트리가 있고 그 하위 트리 안에는 또 다른 하위 트리가 있는 재귀적 자료구조이기도 합니다.
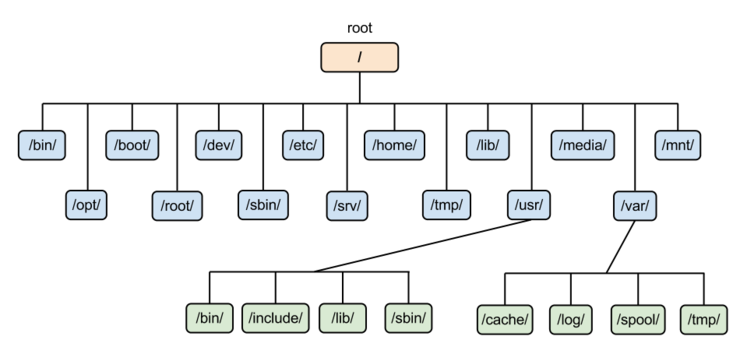
컴퓨터의 direcory구조가 트리 구조의 대표적인 예가 될 수 있습니다.
트리 구조에서 사용되는 기본 용어
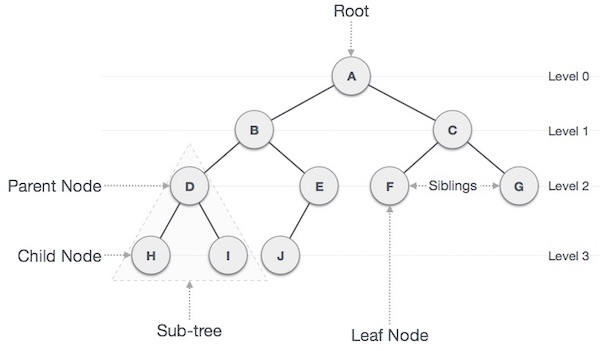
노드 (Node)
- 트리를 구성하고 있는 기본 요소
- 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음.
- A, B, C, D, E, F, G, H, I, J
간선 (Edge)
- 노드와 노드 간의 연결선
루트 노드 (Root Node)
- 트리 구조에서 부모가 없는 최상위 노드
- root node : A
부모 노드 (Parent Node)
- 자식 노드를 가진 노드
- H, I에 부모 노드는 D
자식 노드 (Child node)
- 부모 노드의 하위 노드
- 노드 D의 자식 노드는 H, I
형제 노드 (Sibling node)
- 같은 부모를 가지는 노드
- H, I는 같은 부모를 가지는 형제 노드
외부 노드(external node, outer node), 단말 노드 (terminal node), 리프 노드(leaf node)
- 자식 노드가 없는 노드
- H, I, J, F, G
내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)
- 자식 노드 하나 이상 가진 노드
- A, B, C, D, E
깊이 (depth)
- 루트에서 어떤 노드까지의 간선(Edge) 수
- 루트 노드의 깊이 : 0
- D의 깊이 : 2
높이 (height)
- 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
- 리프 노드의 높이 : 0
- A 노드의 높이 : 3

깊이(depth)와 높이(height) 표현
Level
- 루트에서 어떤 노드까지의 간선(Edge) 수
Degree
- 노드의 자식 수
- Leaf node의 degree : 0; A의 degree : 2
Path
- 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
- A & H 경로 : A-B-D-H
Path Length
- 해당 경로에 있는 총노드의 수
- A & H 경로 길이 : 4
Size
- 자신을 포함한 자손의 노드 수
- 노드 B의 size : 6
Width
- 레벨에 있는 노드 수
- Level 2 width : 4
Breadth
- 리프 노드의 수
- Breadth : 5
Distance
- 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
- D와 J의 Distance : 3
Order
- 부모 노드가 가질 수 있는 최대 자식의 수
- Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다.
특징
트리는 다음과 같은 특징을 가지고 있습니다.
- 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있습니다.
- 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조입니다.
- 트리내에 또 다른 트리가 있는 재귀적 자료구조입니다.
- 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조입니다.
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖습니다.
- 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가집니다.
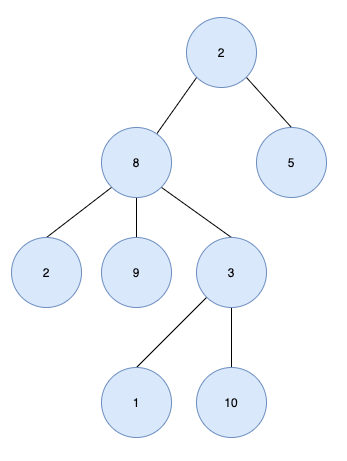
다음은 트리가 아닌 경우입니다.
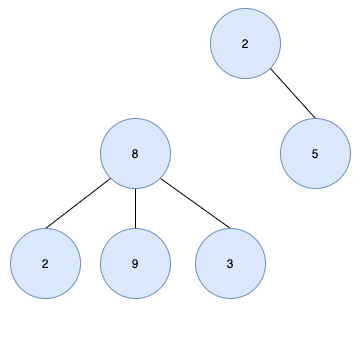
루트 노드가 2개(2, 8) 있으므로 트리가 아닙니다.
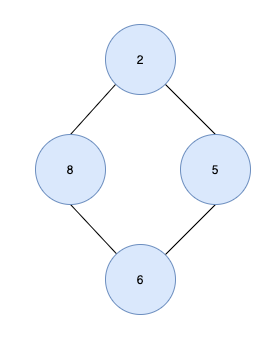
노드 6에는 2명의 부모 노드(8,5)가 있고 사이클(2-8-6-5)이 형성되므로 트리가 아닙니다.
트리 종류
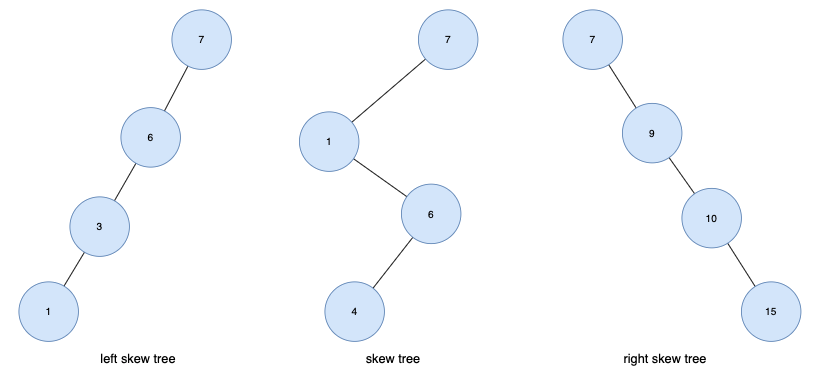
편향 트리 (skew tree)
- 모든 노드들이 자식을 하나만 가진 트리
- 왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree, 오른쪽 방향으로 하나씩만 가질 때 right skew tree라고 함.
이진트리 (Binary Tree)
- 각 노드의 차수(자식 노드)가 2 이하인 트리
이진 탐색 트리 (Binary Search Tree, BST)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함.
m 원 탐색 트리(m-way search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용함.
균형 트리 (Balanced Tree, B-Tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 함.
사용 사례
계층 적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용됩니다.
- 예를 들어 파일 및 폴더는 계층적 트리 형태로 저장됩니다.
효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용합니다.
힙(Heap)
- 힙도 트리로 된 자료 구조입니다.
데이터 베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용합니다.
- 예) B-Tree, B+Tree, AVL-Tree..
Trie
- 사전을 저장하는 데 사용되는 특별한 종류의 트리입니다.
구현방법
링크드 리스트 방법을 이용한다.
각 링크드 리스트 정보에는 부모노드, 자식노드의 정보가 필요하다.
아래와 같은식으로 구현할 수 있다. 실제 코딩테스트에는 나올 확률이 적지만 내부 구조를 알고 있는 것은 중요하다.
public class TreeNode {
private TreeNode left;
private TreeNode right;
private Object data;
public TreeNode(Object item){
left = null;
right = null;
data = item;
}
//자신과 왼쪽 자식 노드(sub)와 연결해주는 method
public void makeLeftSubTree(TreeNode sub){
if(this.left != null) this.left = null;
this.left = sub;
}
//자신과 오른쪽 자식 노드(sub)와 연결해주는 method
public void makeRightSubTree(TreeNode sub){
if(this.right != null) this.right = null;
this.right = sub;
}
//자신의 data를 반환하는 함수
public Object getData(){
return this.data;
}
//자신의 왼쪽 자식노드를 반환하는 함수
public TreeNode getLeftSubTree(){
return this.left;
}
//자신의 오른쪽 자식노드를 반환하는 함수
public TreeNode getRightSubTree(){
return this.right;
}
}
public class main {
public static void main(String[] args) {
TreeNode bt1 = new TreeNode(1);
TreeNode bt2 = new TreeNode(2);
TreeNode bt3 = new TreeNode(3);
TreeNode bt4 = new TreeNode("song");
bt1.makeLeftSubTree(bt2);
bt1.makeRightSubTree(bt3);
bt2.makeLeftSubTree(bt4);
//bt1의 왼쪽 자식노드의 데이터 출력
System.out.println(bt1.getLeftSubTree().getData());
//bt1의 오른쪽 자식노드의 데이터 출력
System.out.println(bt1.getRightSubTree().getData());
}
}
'Computer Science > 자료구조' 카테고리의 다른 글
| 해시 테이블 (0) | 2023.01.09 |
|---|---|
| 이진탐색트리 (0) | 2023.01.09 |
| 그래프 (0) | 2022.12.30 |
| 스택(Stack) (0) | 2022.12.29 |
| 우선순위 큐(Queue) (0) | 2022.12.28 |
정의
트리 (Tree)란 노드들이 나무 가지처럼 연결된 비선형 계층적 자료구조입니다.
트리는 다음과 같이 나무를 거꾸로 뒤집어 놓은 모양과 유사합니다.

트리는 또한 트리 내에 다른 하위 트리가 있고 그 하위 트리 안에는 또 다른 하위 트리가 있는 재귀적 자료구조이기도 합니다.
컴퓨터의 direcory구조가 트리 구조의 대표적인 예가 될 수 있습니다.

트리 구조에서 사용되는 기본 용어

노드 (Node)
- 트리를 구성하고 있는 기본 요소
- 노드에는 키 또는 값과 하위 노드에 대한 포인터를 가지고 있음.
- A, B, C, D, E, F, G, H, I, J
간선 (Edge)
- 노드와 노드 간의 연결선
루트 노드 (Root Node)
- 트리 구조에서 부모가 없는 최상위 노드
- root node : A
부모 노드 (Parent Node)
- 자식 노드를 가진 노드
- H, I에 부모 노드는 D
자식 노드 (Child node)
- 부모 노드의 하위 노드
- 노드 D의 자식 노드는 H, I
형제 노드 (Sibling node)
- 같은 부모를 가지는 노드
- H, I는 같은 부모를 가지는 형제 노드
외부 노드(external node, outer node), 단말 노드 (terminal node), 리프 노드(leaf node)
- 자식 노드가 없는 노드
- H, I, J, F, G
내부 노드 (internal node, inner node), 비 단말 노드 (non-terminal node), 가지 노드 (branch node)
- 자식 노드 하나 이상 가진 노드
- A, B, C, D, E
깊이 (depth)
- 루트에서 어떤 노드까지의 간선(Edge) 수
- 루트 노드의 깊이 : 0
- D의 깊이 : 2
높이 (height)
- 어떤 노드에서 리프 노드까지 가장 긴 경로의 간선(Edge) 수
- 리프 노드의 높이 : 0
- A 노드의 높이 : 3

깊이(depth)와 높이(height) 표현
Level
- 루트에서 어떤 노드까지의 간선(Edge) 수
Degree
- 노드의 자식 수
- Leaf node의 degree : 0; A의 degree : 2
Path
- 한 노드에서 다른 한 노드에 이르는 길 사이에 놓여있는 노드들의 순서
- A & H 경로 : A-B-D-H
Path Length
- 해당 경로에 있는 총노드의 수
- A & H 경로 길이 : 4
Size
- 자신을 포함한 자손의 노드 수
- 노드 B의 size : 6
Width
- 레벨에 있는 노드 수
- Level 2 width : 4
Breadth
- 리프 노드의 수
- Breadth : 5
Distance
- 두 노드 사이의 최단 경로에 있는 간선(Edge)의 수
- D와 J의 Distance : 3
Order
- 부모 노드가 가질 수 있는 최대 자식의 수
- Order 3 : 부모 노드는 최대 3명의 자식을 가질 수 있다.
특징
트리는 다음과 같은 특징을 가지고 있습니다.
- 하나의 루트 노드와 0개 이상의 하위 트리로 구성되어 있습니다.
- 데이터를 순차적으로 저장하지 않기 때문에 비선형 자료구조입니다.
- 트리내에 또 다른 트리가 있는 재귀적 자료구조입니다.
- 단순 순환(Loop)을 갖지 않고, 연결된 무방향 그래프 구조입니다.
- 노드 간에 부모 자식 관계를 갖고 있는 계층형 자료구조이며 모든 자식 노드는 하나의 부모 노드만 갖습니다.
- 노드가 n개인 트리는 항상 n-1개의 간선(edge)을 가집니다.

다음은 트리가 아닌 경우입니다.

루트 노드가 2개(2, 8) 있으므로 트리가 아닙니다.

노드 6에는 2명의 부모 노드(8,5)가 있고 사이클(2-8-6-5)이 형성되므로 트리가 아닙니다.
트리 종류
편향 트리 (skew tree)
- 모든 노드들이 자식을 하나만 가진 트리
- 왼쪽 방향으로 자식을 하나씩만 가질 때 left skew tree, 오른쪽 방향으로 하나씩만 가질 때 right skew tree라고 함.

이진트리 (Binary Tree)
- 각 노드의 차수(자식 노드)가 2 이하인 트리
이진 탐색 트리 (Binary Search Tree, BST)
- 순서화된 이진 트리
- 노드의 왼쪽 자식은 부모의 값보다 작은 값을 가져야 하며 노드의 오른쪽 자식은 부모의 값보다 큰 값을 가져야 함.
m 원 탐색 트리(m-way search tree)
- 최대 m개의 서브 트리를 갖는 탐색 트리
- 이진 탐색 트리의 확장된 형태로 높이를 줄이기 위해 사용함.
균형 트리 (Balanced Tree, B-Tree)
- m원 탐색 트리에서 높이 균형을 유지하는 트리
- height-balanced m-way tree라고도 함.
사용 사례
계층 적 데이터 저장
- 트리는 데이터를 계층 구조로 저장하는 데 사용됩니다.
- 예를 들어 파일 및 폴더는 계층적 트리 형태로 저장됩니다.
효율적인 검색 속도
- 효율적인 삽입, 삭제 및 검색을 위해 트리 구조를 사용합니다.
힙(Heap)
- 힙도 트리로 된 자료 구조입니다.
데이터 베이스 인덱싱
- 데이터베이스 인덱싱을 구현하는데 트리를 사용합니다.
- 예) B-Tree, B+Tree, AVL-Tree..
Trie
- 사전을 저장하는 데 사용되는 특별한 종류의 트리입니다.
구현방법
링크드 리스트 방법을 이용한다.
각 링크드 리스트 정보에는 부모노드, 자식노드의 정보가 필요하다.
아래와 같은식으로 구현할 수 있다. 실제 코딩테스트에는 나올 확률이 적지만 내부 구조를 알고 있는 것은 중요하다.
public class TreeNode {
private TreeNode left;
private TreeNode right;
private Object data;
public TreeNode(Object item){
left = null;
right = null;
data = item;
}
//자신과 왼쪽 자식 노드(sub)와 연결해주는 method
public void makeLeftSubTree(TreeNode sub){
if(this.left != null) this.left = null;
this.left = sub;
}
//자신과 오른쪽 자식 노드(sub)와 연결해주는 method
public void makeRightSubTree(TreeNode sub){
if(this.right != null) this.right = null;
this.right = sub;
}
//자신의 data를 반환하는 함수
public Object getData(){
return this.data;
}
//자신의 왼쪽 자식노드를 반환하는 함수
public TreeNode getLeftSubTree(){
return this.left;
}
//자신의 오른쪽 자식노드를 반환하는 함수
public TreeNode getRightSubTree(){
return this.right;
}
}
public class main {
public static void main(String[] args) {
TreeNode bt1 = new TreeNode(1);
TreeNode bt2 = new TreeNode(2);
TreeNode bt3 = new TreeNode(3);
TreeNode bt4 = new TreeNode("song");
bt1.makeLeftSubTree(bt2);
bt1.makeRightSubTree(bt3);
bt2.makeLeftSubTree(bt4);
//bt1의 왼쪽 자식노드의 데이터 출력
System.out.println(bt1.getLeftSubTree().getData());
//bt1의 오른쪽 자식노드의 데이터 출력
System.out.println(bt1.getRightSubTree().getData());
}
}
'Computer Science > 자료구조' 카테고리의 다른 글
| 해시 테이블 (0) | 2023.01.09 |
|---|---|
| 이진탐색트리 (0) | 2023.01.09 |
| 그래프 (0) | 2022.12.30 |
| 스택(Stack) (0) | 2022.12.29 |
| 우선순위 큐(Queue) (0) | 2022.12.28 |
