정의
연결되어 있는 객체 간의 관계를 표현하는 비선형 자료구조
가장 일반적인 자료구조의 형태로, tree도 그래프의 특수한 경우이다. 예를 들면, 전기회로의 소자 간 연결 상태나 혹은 운영체제의 프로세스와 자원 관계 또한 그래프로 표현이 가능하다.
그래프의 종류
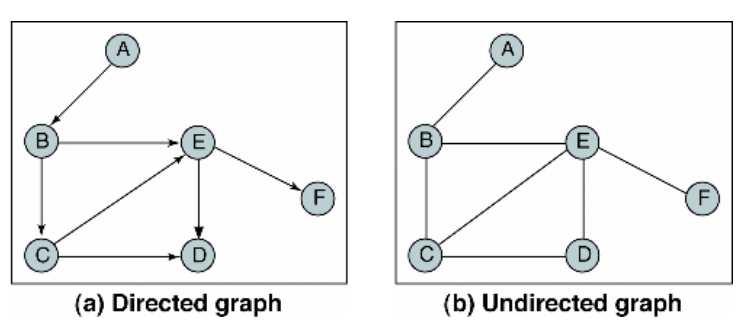
1) 무향 그래프 (undirected graph)
: 무향 에지는 양방향의 의미임. 예컨대 조합(combination)처럼 (A,B) = (B,A)로 순서에 의미가 없다는 것.
2) 방향 그래프 (directed graph)
: 에지를 통해서 한쪽 방향으로만 갈 수 있다는 특징. 즉, <A.B> ≠ <B,A> 라는 특성을 보임.
cf.) 가중치 그래프: 각 간선에 가중치를 부여한 형태의 그래프. 예를 들면 edge에 비용을 부과하는 형식으로 가중치가 부과될 수 있음.
차수
한 노드에 이어져 있는 간선의 수를 차수 (degree) 라고 한다. 차수가 0인 노드는 고립 (isolated) 되었다고 한다. 유향 그래프의 경우, 입력 차수 (in-degree) 와 출력 차수 (out-degree) 로 나눌 수 있으며, 각각 노드로 들어오는 간선과 노드에서 나가는 간선의 수를 뜻한다.
경로, 보행, 순환
그래프에서 경로 (path) 는 간선이 어느 노드도 다시 방문하지 않고 노드가 일렬로 연결된 부분 그래프다. 유향 그래프에서 경로는 간선의 방향을 따른다.
보행 (walk) 은 노드와 간선을 번갈아 가며 반복적으로 방문하는 노드와 간선이다. 경로는 노드와 간선이 모두 중복되지 않는 보행과 같다 (즉, 경로의 상위 집합이다).
순환 (cycle) 은 경로와 같으나 마지막에 연결된 간선의 노드가 다시 첫 번째 노드에 연결된다.
경로 또는 보행의 길이 (length) 는 지나가는 간선의 수를 뜻한다.
구현 방법
1. 인접행렬
adjacency matrix: 인접한 정점들의 상태를 행렬(2차원 배열)로 구성.
인접하면 1이다.
같은 노드끼리는 0이다.
연결되지 않은 노드끼리는 0 또는 무한대 inf로 표현한다.
adjac_matrix = [[0, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 1, 0, 0, 0],
[1, 0, 0, 0, 1, 1, 0],
[0, 1, 0, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0]]
- Directed graph의 경우 진입차수(방향을 맞은?방향)의 차수를 입력한다.
- Undirected의 인접행렬은 대칭행렬(symmetric matrix)다.
- 😥Node가 많아지면 메모리가 n2 배로 필요해진다.
- 두개의 노드가 연결되어있는지 확인여부만 체크할 때는 O(1)의 복잡도이다.
2.인접리스트
# vertext list
vert_lst = ['0', '1', '2', '3', '4', '5', '6']
# edge list
edge_lst = [(0, 1), (1, 0), (1, 3), (3, 1), (3, 6), (6, 3), (0, 2), (2, 0), (2, 4), (4, 2), (2, 5), (5, 2)]
# adjacency list
adjac_lst = [[] for vert in vert_lst]
for edge in edge_lst:
adjac_lst[edge[0]].append(edge[1])
print(adjac_lst) # [[1, 2], [0, 3], [0, 4, 5], [1, 6], [2], [2], [3]]
결과로 정점 0 부터 6까지 인접한 정점들의 집합이 나온다.
이 인접한 정점들의 집합과 스택 쿠조를 이용하여 visited(flag) list를 만들어 그래프를 모두 탐색한다.
def stack_graph(adjac_lst):
stack = [0]
visit_vert = []
while stack:
current = stack.pop()
for neighbor in adjac_lst[current]:
if neighbor not in visit_vert:
stack.append(neighbor)
visit_vert.append(current)
return visit_vert-인접리스트는 검색,탐색에서 불리하다.
- 인접리스트의 구현 in Python
파이썬은 포인터가 따로 존재하지 않으므로, 연결리스트를 구현하기 까다롭다. 따라서 인접 리스트를 출발 노드를 키로, 도착 노드를 값으로 표현하는 딕셔너리 형태로 표현한다. 도착 노드의 경우에는 여러 개의 노드가 가능하므로 값은 리스트 형태로 표현한다.
'Computer Science > 자료구조' 카테고리의 다른 글
| 이진탐색트리 (0) | 2023.01.09 |
|---|---|
| 트리 (0) | 2023.01.02 |
| 스택(Stack) (0) | 2022.12.29 |
| 우선순위 큐(Queue) (0) | 2022.12.28 |
| 큐(Queue,deque,list) (0) | 2022.12.28 |
정의
연결되어 있는 객체 간의 관계를 표현하는 비선형 자료구조
가장 일반적인 자료구조의 형태로, tree도 그래프의 특수한 경우이다. 예를 들면, 전기회로의 소자 간 연결 상태나 혹은 운영체제의 프로세스와 자원 관계 또한 그래프로 표현이 가능하다.
그래프의 종류
1) 무향 그래프 (undirected graph)
: 무향 에지는 양방향의 의미임. 예컨대 조합(combination)처럼 (A,B) = (B,A)로 순서에 의미가 없다는 것.
2) 방향 그래프 (directed graph)
: 에지를 통해서 한쪽 방향으로만 갈 수 있다는 특징. 즉, <A.B> ≠ <B,A> 라는 특성을 보임.

cf.) 가중치 그래프: 각 간선에 가중치를 부여한 형태의 그래프. 예를 들면 edge에 비용을 부과하는 형식으로 가중치가 부과될 수 있음.
차수
한 노드에 이어져 있는 간선의 수를 차수 (degree) 라고 한다. 차수가 0인 노드는 고립 (isolated) 되었다고 한다. 유향 그래프의 경우, 입력 차수 (in-degree) 와 출력 차수 (out-degree) 로 나눌 수 있으며, 각각 노드로 들어오는 간선과 노드에서 나가는 간선의 수를 뜻한다.
경로, 보행, 순환
그래프에서 경로 (path) 는 간선이 어느 노드도 다시 방문하지 않고 노드가 일렬로 연결된 부분 그래프다. 유향 그래프에서 경로는 간선의 방향을 따른다.
보행 (walk) 은 노드와 간선을 번갈아 가며 반복적으로 방문하는 노드와 간선이다. 경로는 노드와 간선이 모두 중복되지 않는 보행과 같다 (즉, 경로의 상위 집합이다).
순환 (cycle) 은 경로와 같으나 마지막에 연결된 간선의 노드가 다시 첫 번째 노드에 연결된다.
경로 또는 보행의 길이 (length) 는 지나가는 간선의 수를 뜻한다.
구현 방법
1. 인접행렬
adjacency matrix: 인접한 정점들의 상태를 행렬(2차원 배열)로 구성.
인접하면 1이다.
같은 노드끼리는 0이다.
연결되지 않은 노드끼리는 0 또는 무한대 inf로 표현한다.
adjac_matrix = [[0, 1, 1, 0, 0, 0, 0],
[1, 0, 0, 1, 0, 0, 0],
[1, 0, 0, 0, 1, 1, 0],
[0, 1, 0, 0, 0, 0, 1],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 1, 0, 0, 0, 0],
[0, 0, 0, 1, 0, 0, 0]]
- Directed graph의 경우 진입차수(방향을 맞은?방향)의 차수를 입력한다.
- Undirected의 인접행렬은 대칭행렬(symmetric matrix)다.
- 😥Node가 많아지면 메모리가 n2 배로 필요해진다.
- 두개의 노드가 연결되어있는지 확인여부만 체크할 때는 O(1)의 복잡도이다.
2.인접리스트
# vertext list
vert_lst = ['0', '1', '2', '3', '4', '5', '6']
# edge list
edge_lst = [(0, 1), (1, 0), (1, 3), (3, 1), (3, 6), (6, 3), (0, 2), (2, 0), (2, 4), (4, 2), (2, 5), (5, 2)]
# adjacency list
adjac_lst = [[] for vert in vert_lst]
for edge in edge_lst:
adjac_lst[edge[0]].append(edge[1])
print(adjac_lst) # [[1, 2], [0, 3], [0, 4, 5], [1, 6], [2], [2], [3]]
결과로 정점 0 부터 6까지 인접한 정점들의 집합이 나온다.
이 인접한 정점들의 집합과 스택 쿠조를 이용하여 visited(flag) list를 만들어 그래프를 모두 탐색한다.
def stack_graph(adjac_lst):
stack = [0]
visit_vert = []
while stack:
current = stack.pop()
for neighbor in adjac_lst[current]:
if neighbor not in visit_vert:
stack.append(neighbor)
visit_vert.append(current)
return visit_vert-인접리스트는 검색,탐색에서 불리하다.
- 인접리스트의 구현 in Python
파이썬은 포인터가 따로 존재하지 않으므로, 연결리스트를 구현하기 까다롭다. 따라서 인접 리스트를 출발 노드를 키로, 도착 노드를 값으로 표현하는 딕셔너리 형태로 표현한다. 도착 노드의 경우에는 여러 개의 노드가 가능하므로 값은 리스트 형태로 표현한다.
'Computer Science > 자료구조' 카테고리의 다른 글
| 이진탐색트리 (0) | 2023.01.09 |
|---|---|
| 트리 (0) | 2023.01.02 |
| 스택(Stack) (0) | 2022.12.29 |
| 우선순위 큐(Queue) (0) | 2022.12.28 |
| 큐(Queue,deque,list) (0) | 2022.12.28 |
