IMOS (いもす法, imos法)
정의
누적합 문제에서 쓸 수 있는 개념
정해진 구간 내에 시작과 끝이 포함된 부분 집합에 대한 명령이 여러개 들어올 때, 반복적으로 연산하게 되면 연산 시간이 매우 커질 수 있다.
예시문제) 도서관 좌석 예약된 수time[0]~time[100000] 의 시간이 있다.입력으로는 각 개개인의 좌석예약시작시간과 종료시간이 들어온다.이를 time[i]+=1로 수행하면 정확도는 통과하지만 속도가 무지하게 느려질 수 있다.이때 효율적으로 사용할 수 있는 것이 imos알고리즘이다.
Imos의 시간복잡도는 배열의 길이이다. 1차원: O(H), 2차원: O(HW) (H:가로, W:세로)
1차원에서의 구현 방법
시작시간과 끝시간을 기록하여 준다.
먼저 각 시간에 대한 1차원 배열을 생성하고 값을 0으로 초기화 해준다. 그 후 각 명령에 대해 시작시간에 +1, 종료시간에 -1을 해준다.
만약 A(1시 ~ 4시), B(2시 ~ 8시), C(3시 ~ 12시), D(4시 ~ 8시) 이라면 배열의 값은 [0,1,1,1,0,0,0,0,-2,0,0,-1] 이 된다.배열은 만든 후 배열크기만큼 반복문을 돌리면 효율성 있게 답을 구할 수 있다.
imos = [0,1,1,1,0,0,0,0,-2,0,0,-1]
now = 0
for i in range(12):
now += imos[i]
imos[i] = now
2차원에서의 구현 방법(효율성 매우 좋음)
효율성을 생각하지 않는다면, 매 입력이 들어올 때마다 해당 사각형 영역에 1씩 직접 다 더해주고, 마지막에 출력만 해 주는 로직을 떠올려보자. 쿼리당 O(HW)만큼 걸리고, 총 시간복잡도는 O(QHW)이다. (H×W 크기의 격자 보드, Q개의 입력)
2차원 배열의 경우는 명령이 2차원 배열로 들어오기 때문에 사각형 모양에서의 각 꼭지점을 시작과 끝으로 생각해서 구현할 수 있다
1. 사각형이 시작하는 부분 (왼쪽 위 점) : +1
2. 시작 부분에서 가로, 세로로 나아갔을 때 범위가 끝나는 부분 (빨간색 표시 지점) : -1
3. 사각형이 끝난 부분 (구간 밖 오른쪽 아래 점) -1 해준 걸 상쇄하기 위해 다시 : +1
이런 방식으로 배열을 생성해주고 다시 값을 계산해줄 때에는 가로와 세로를 나눠서 두 번 반복문을 돌려준다.(마지막에!)
사각형으로 바뀌어도 기본적인 아이디어는 같다. "시작과 끝만 기록한다" 단 2차원에서는 차원이 늘어난 만큼, 가로 방향으로 시작과 끝, 세로 방향으로 시작과 끝 두 번 기록하고, 시뮬레이팅할 때도 가로로 한번, 세로로 한번 휩쓸면 된다.

먼저 가로로 반복문을 돌리면

세로로 반복문을 돌리면

for i in range(len(imos)):
now = 0
for j in range(len(imos[0])):
now += imos[i][j]
imos[i][j] = now
for i in range(len(imos[0])):
now = 0
for j in range(len(imos)):
now += imos[j][i]
imos[j][i] = now


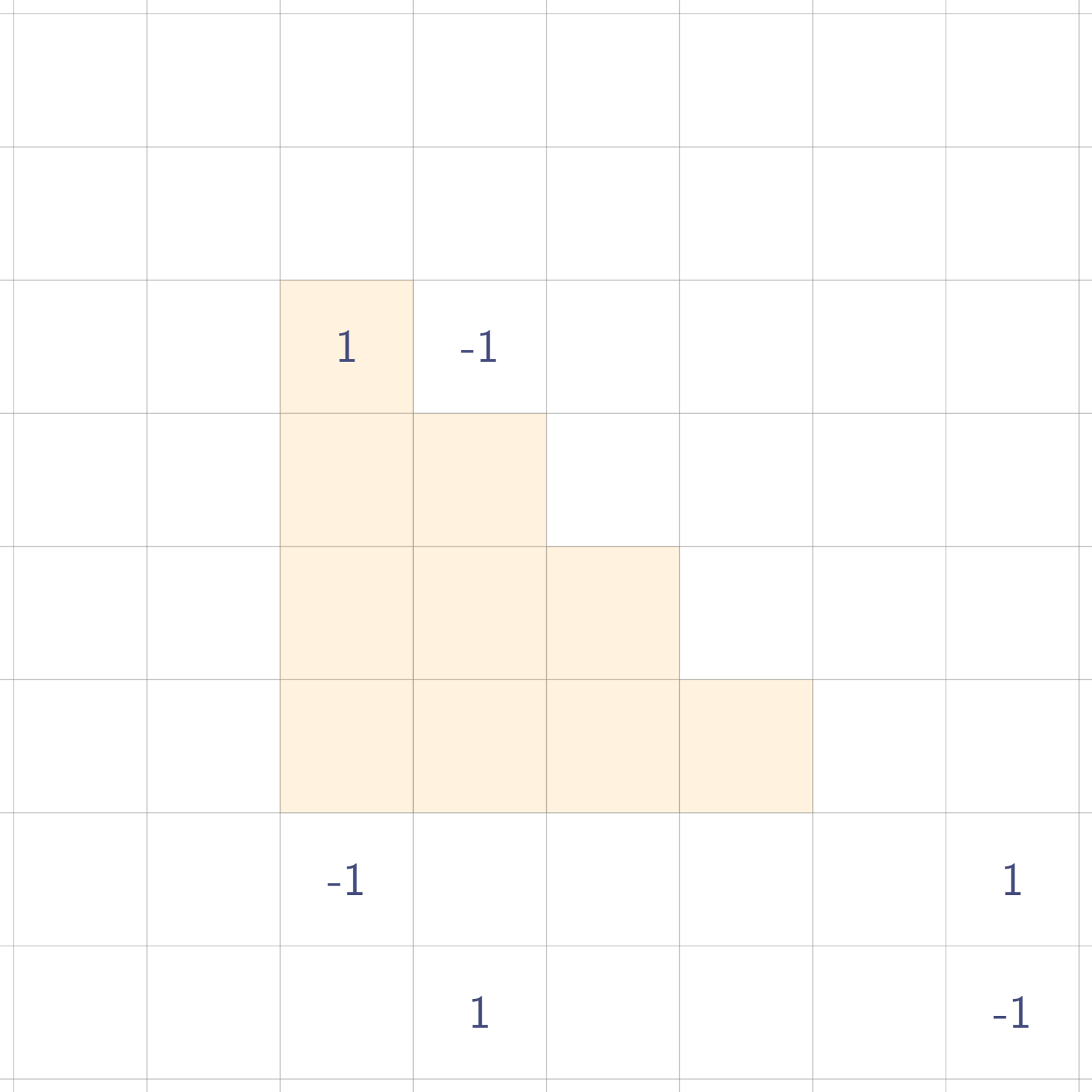
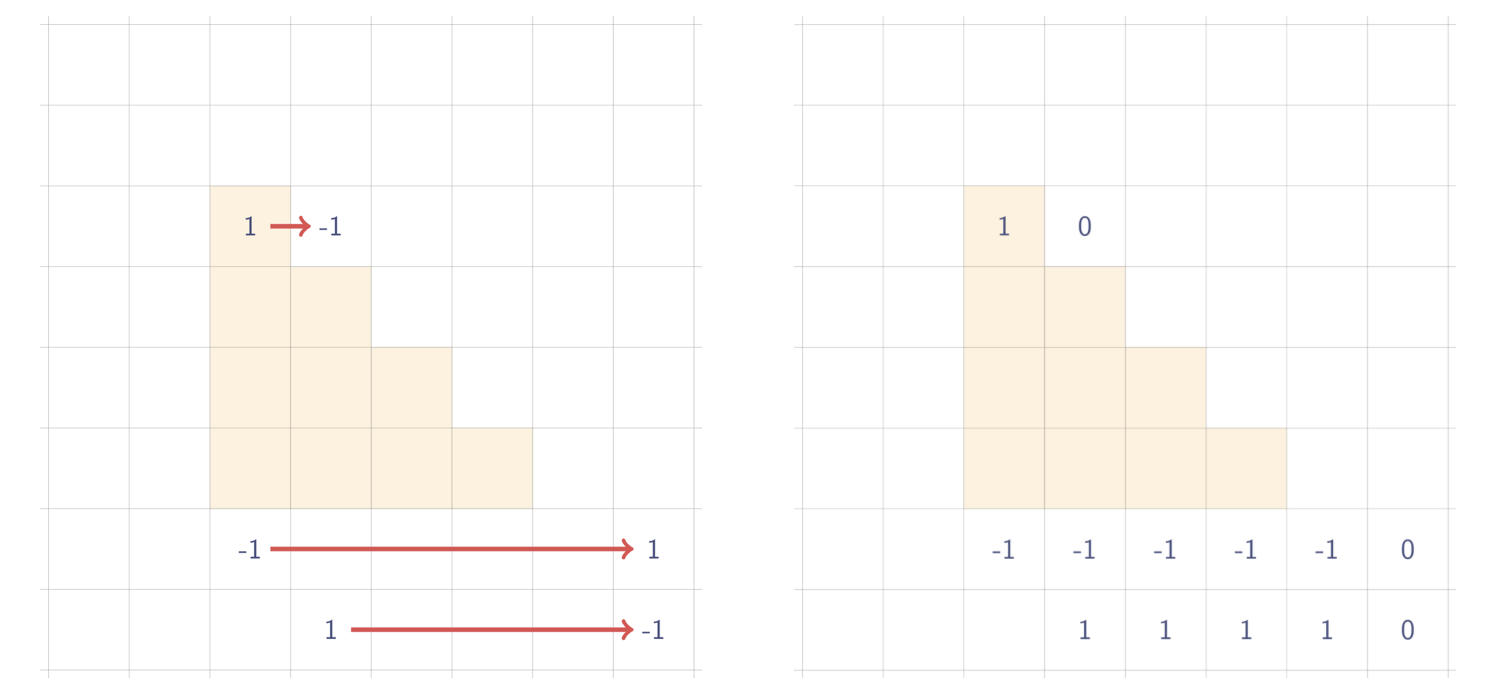
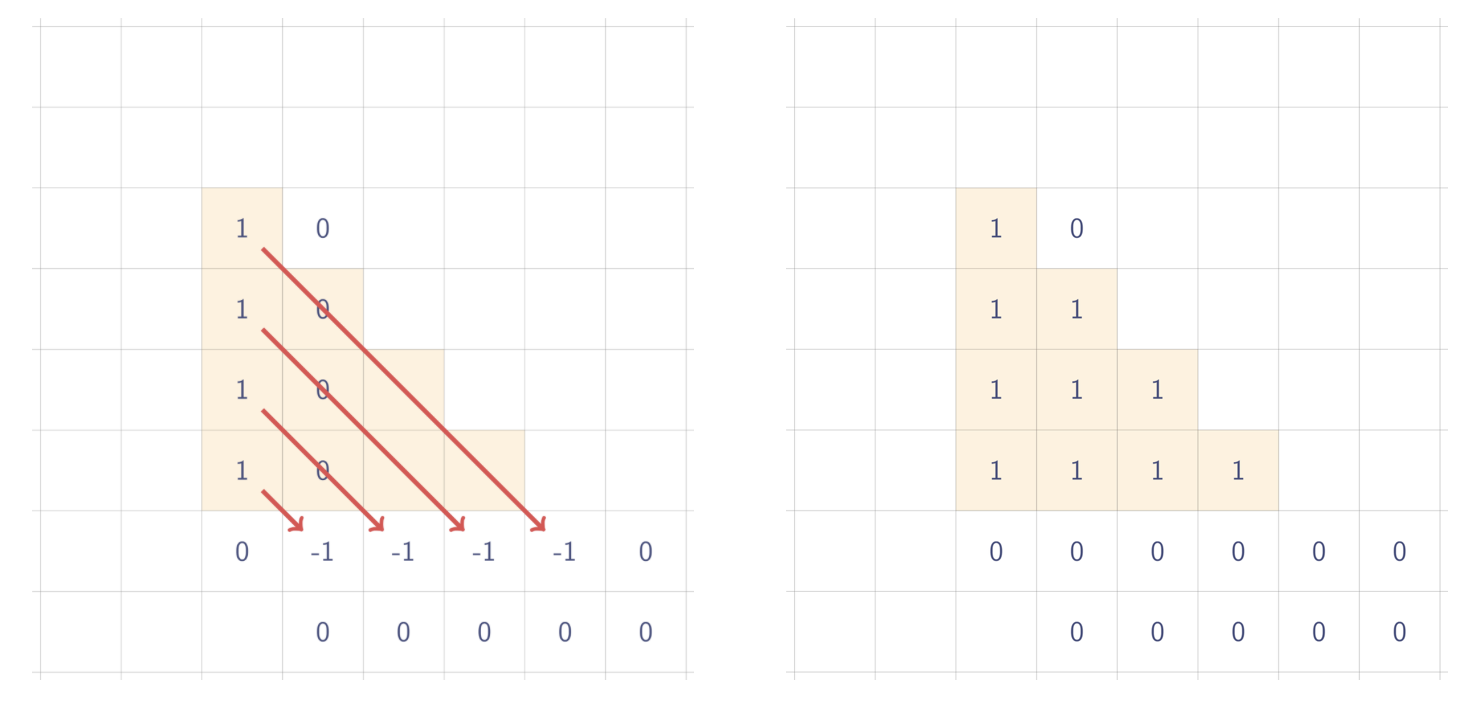
2차원에서의 삼각형 구현 방법(특수좌표계)
삼각형은 6개의 점이 필요하고 세번 휩쓸어야 한다.


참고: https://velog.io/@nkrang/알고리즘-imos-법 , https://driip.me/65d9b58c-bf02-44bf-8fba-54d394ed21e0
'Computer Science > 알고리즘' 카테고리의 다른 글
| 투포인터 (0) | 2023.05.02 |
|---|---|
| 최단경로(다익스트라,플로이드워셜) (1) | 2023.01.19 |
| 다이나믹 프로그래밍 (0) | 2023.01.12 |
| 이진 탐색 (0) | 2023.01.09 |
| 정렬 (0) | 2023.01.04 |
IMOS (いもす法, imos法)
정의
누적합 문제에서 쓸 수 있는 개념
정해진 구간 내에 시작과 끝이 포함된 부분 집합에 대한 명령이 여러개 들어올 때, 반복적으로 연산하게 되면 연산 시간이 매우 커질 수 있다.
예시문제) 도서관 좌석 예약된 수time[0]~time[100000] 의 시간이 있다.입력으로는 각 개개인의 좌석예약시작시간과 종료시간이 들어온다.이를 time[i]+=1로 수행하면 정확도는 통과하지만 속도가 무지하게 느려질 수 있다.이때 효율적으로 사용할 수 있는 것이 imos알고리즘이다.
Imos의 시간복잡도는 배열의 길이이다. 1차원: O(H), 2차원: O(HW) (H:가로, W:세로)
1차원에서의 구현 방법
시작시간과 끝시간을 기록하여 준다.
먼저 각 시간에 대한 1차원 배열을 생성하고 값을 0으로 초기화 해준다. 그 후 각 명령에 대해 시작시간에 +1, 종료시간에 -1을 해준다.
만약 A(1시 ~ 4시), B(2시 ~ 8시), C(3시 ~ 12시), D(4시 ~ 8시) 이라면 배열의 값은 [0,1,1,1,0,0,0,0,-2,0,0,-1] 이 된다.배열은 만든 후 배열크기만큼 반복문을 돌리면 효율성 있게 답을 구할 수 있다.
imos = [0,1,1,1,0,0,0,0,-2,0,0,-1]
now = 0
for i in range(12):
now += imos[i]
imos[i] = now
2차원에서의 구현 방법(효율성 매우 좋음)
효율성을 생각하지 않는다면, 매 입력이 들어올 때마다 해당 사각형 영역에 1씩 직접 다 더해주고, 마지막에 출력만 해 주는 로직을 떠올려보자. 쿼리당 O(HW)만큼 걸리고, 총 시간복잡도는 O(QHW)이다. (H×W 크기의 격자 보드, Q개의 입력)
2차원 배열의 경우는 명령이 2차원 배열로 들어오기 때문에 사각형 모양에서의 각 꼭지점을 시작과 끝으로 생각해서 구현할 수 있다
1. 사각형이 시작하는 부분 (왼쪽 위 점) : +1
2. 시작 부분에서 가로, 세로로 나아갔을 때 범위가 끝나는 부분 (빨간색 표시 지점) : -1
3. 사각형이 끝난 부분 (구간 밖 오른쪽 아래 점) -1 해준 걸 상쇄하기 위해 다시 : +1
이런 방식으로 배열을 생성해주고 다시 값을 계산해줄 때에는 가로와 세로를 나눠서 두 번 반복문을 돌려준다.(마지막에!)
사각형으로 바뀌어도 기본적인 아이디어는 같다. "시작과 끝만 기록한다" 단 2차원에서는 차원이 늘어난 만큼, 가로 방향으로 시작과 끝, 세로 방향으로 시작과 끝 두 번 기록하고, 시뮬레이팅할 때도 가로로 한번, 세로로 한번 휩쓸면 된다.

먼저 가로로 반복문을 돌리면

세로로 반복문을 돌리면

for i in range(len(imos)):
now = 0
for j in range(len(imos[0])):
now += imos[i][j]
imos[i][j] = now
for i in range(len(imos[0])):
now = 0
for j in range(len(imos)):
now += imos[j][i]
imos[j][i] = now


2차원에서의 삼각형 구현 방법(특수좌표계)
삼각형은 6개의 점이 필요하고 세번 휩쓸어야 한다.





참고: https://velog.io/@nkrang/알고리즘-imos-법 , https://driip.me/65d9b58c-bf02-44bf-8fba-54d394ed21e0
'Computer Science > 알고리즘' 카테고리의 다른 글
| 투포인터 (0) | 2023.05.02 |
|---|---|
| 최단경로(다익스트라,플로이드워셜) (1) | 2023.01.19 |
| 다이나믹 프로그래밍 (0) | 2023.01.12 |
| 이진 탐색 (0) | 2023.01.09 |
| 정렬 (0) | 2023.01.04 |
